Word Shapes
Comparing Words by the Letter-Adjacency Graphs.
This video by John Turner has a fun idea: Looking at which words are ‘shaped’ the same. One of the ways he defines a word’s shape is via its graph1 of letter adjacencies. For example, “baboon” and “refers” have the same graph shape because the network of connections between adjacent letters is similar.
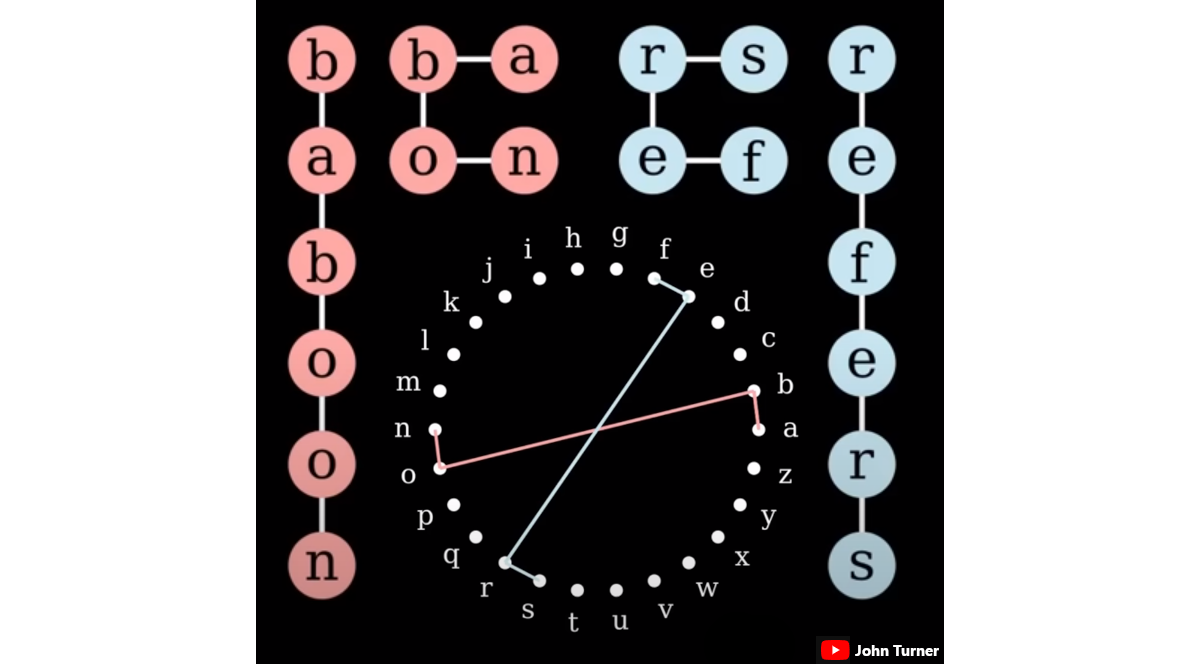
Unfortunately, despite using a graphing library called Scott to compute canonical representations of each word’s graph, what Turner has calculated doesn’t seem to actually be (just) about graph isomorphism. It also takes into account the position of letters around the “letter wheel”. I found this unsatisfyingly restrictive.
Looking at just the networks of letter adjacency, “baboon” should be similar not just to words like “refers”, but also to words like “cats” and “wooly”.
The video made me curious what the results would look like when looking at just the graph of adjcencies between letters in a word. (Henceforce “the word’s graph” for short.)
This post partially answers that question
using the enable1 dictionary of words from this Github Repo
Which Small Graphs are Missing?
4 or fewer nodes
If we’re looking at words with four or fewer distinct letters, there are only a few ‘shapes’ such a word graph could have. (20, to be precise.) And every one of them has at least one corresponding word.
In fact, all of them except for the K4 complete graph have multiple words. K4 only has one, and it’s a bit iffy. It’s “gensengs”, which is the plural of an alternate spelling of “ginseng”.
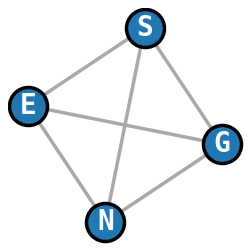
Should that count? well, it’s in the dictionary I’m using, so 🤷
5 nodes
Of the 21 simple connected graphs with 5 nodes, all are represented except for one. The missing graph is K5, aka the pentatope graph.

No word has this graph. I also checked the larger words and none of them seem to contain this shape as a subgraph either. Spooky!
Here’s a table showing all the graphs with 5 or fewer nodes.
| Graph | Example Word | Visualization |
|---|---|---|
| singleton graph | i |  |
| 2-path | to |  |
| 3-path | air | 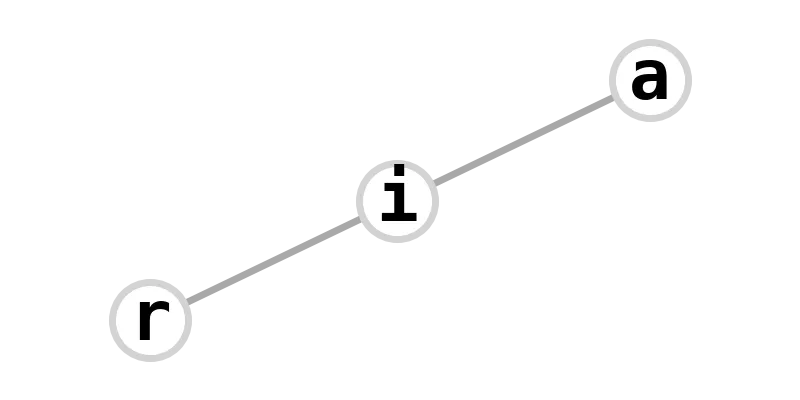 |
| K3 (triangle) | aqua | 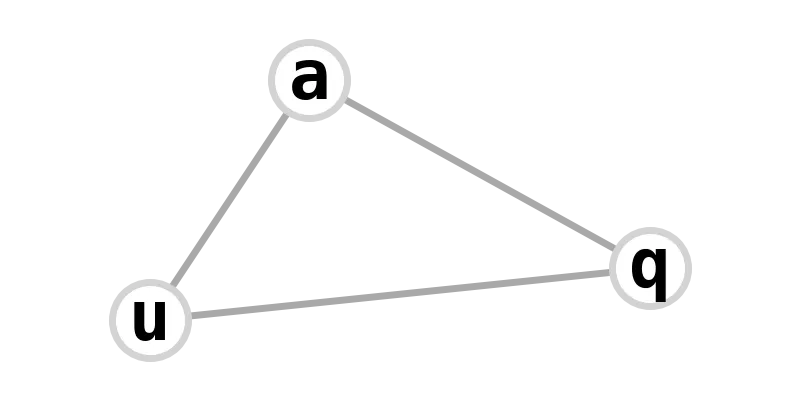 |
| paw graph | catch | 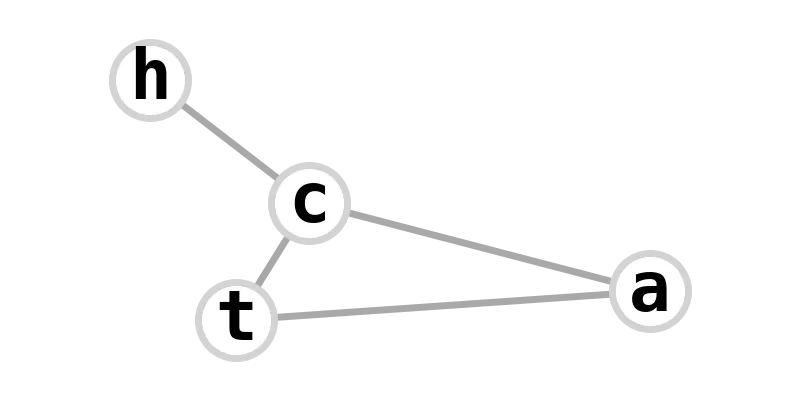 |
| 4-path | fire | 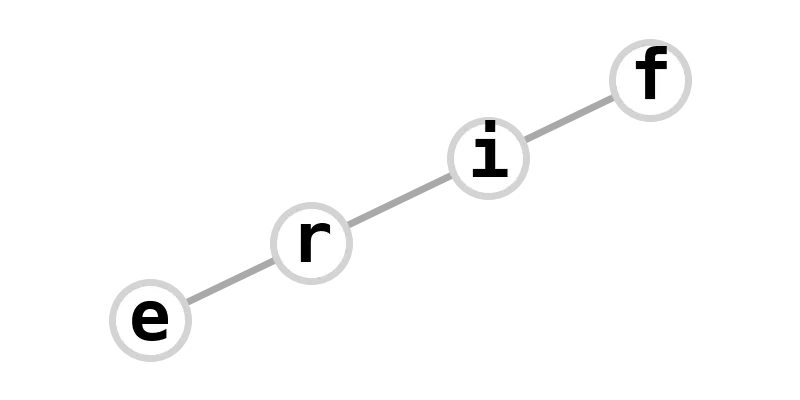 |
| diamond graph | miasma | 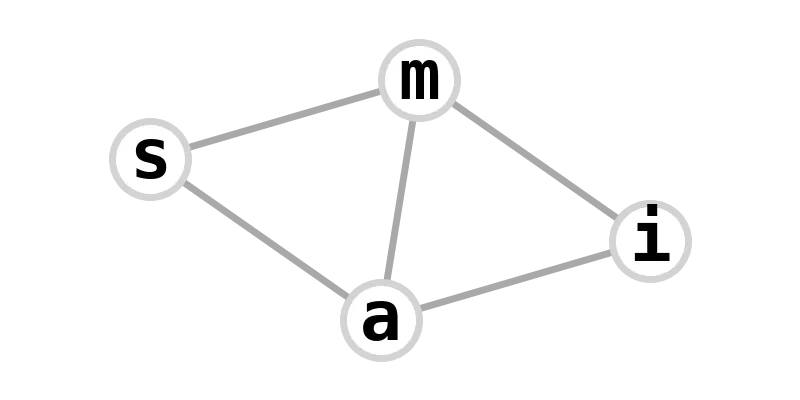 |
| square graph | anima | 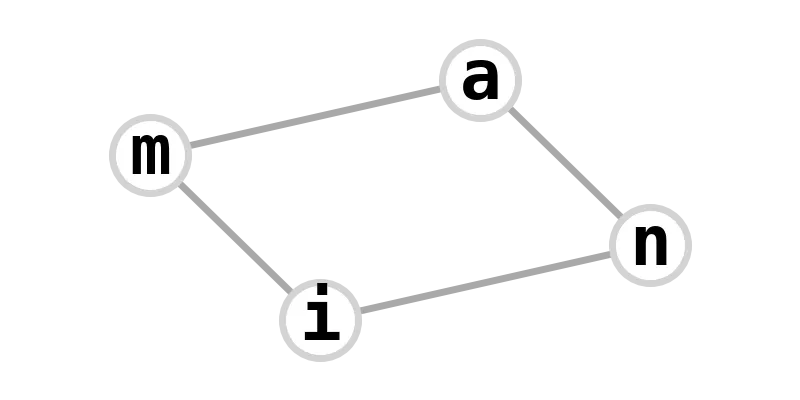 |
| K4 (tetrahedron) | gensengs | 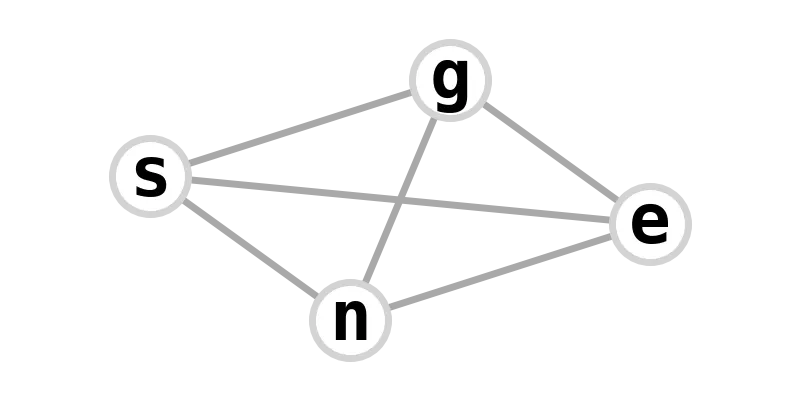 |
| banner graph | absorb | 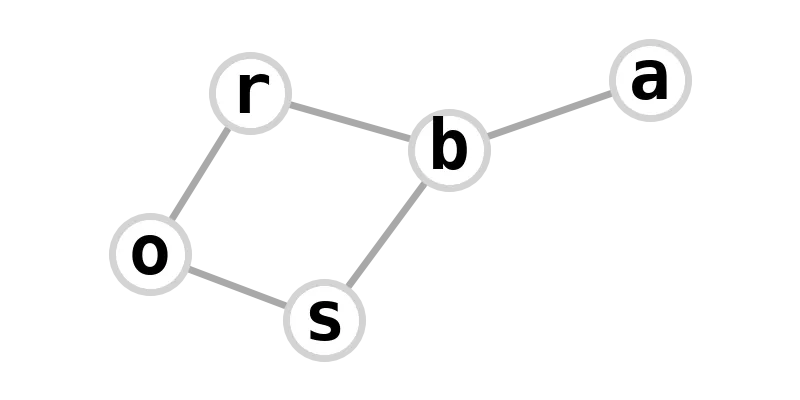 |
| fork graph | elixir | 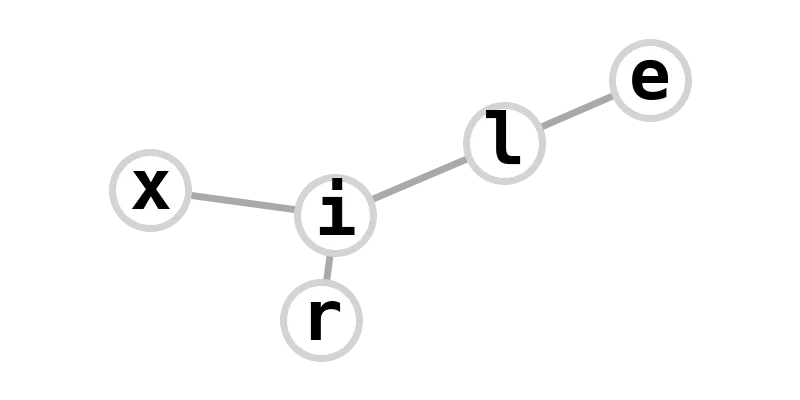 |
| (3,2)-tadpole graph | propel | 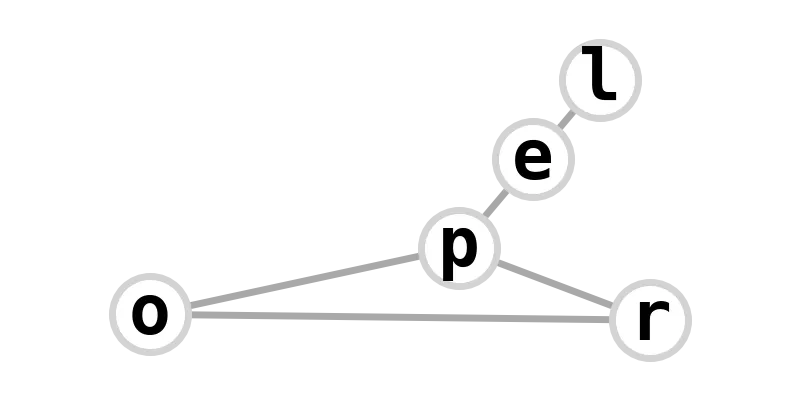 |
| bull graph | alcohol | 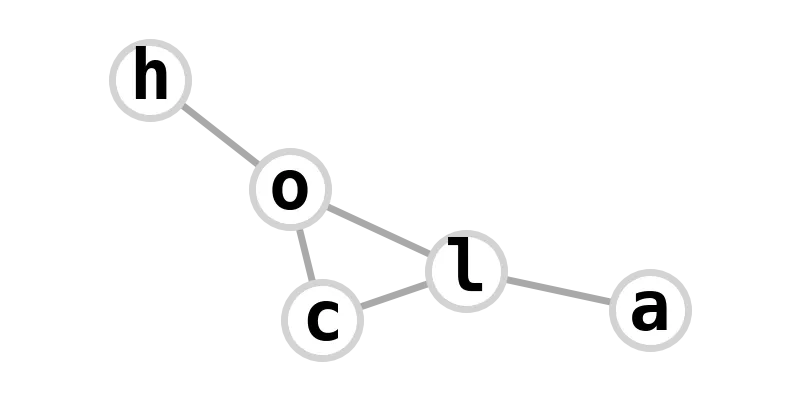 |
| kite graph | calculus | 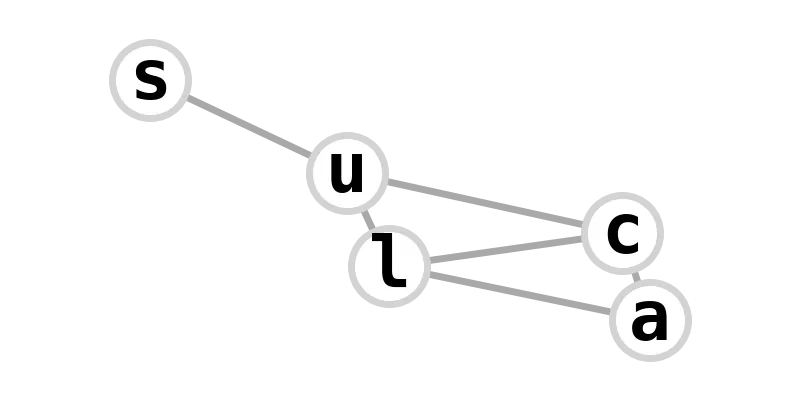 |
| butterfly graph | tempest | 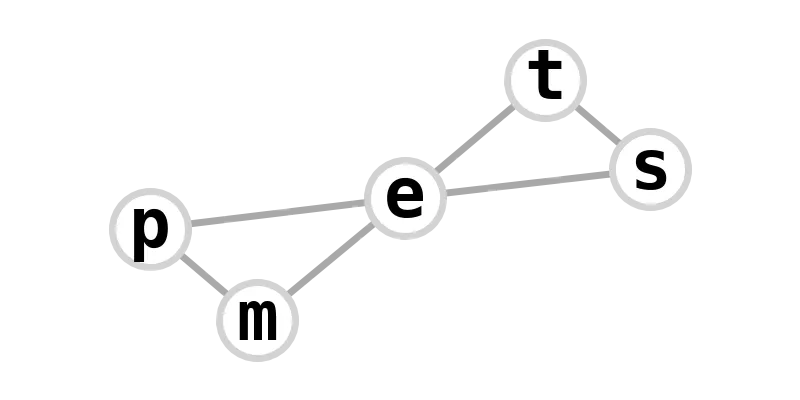 |
| (4,1)-lollipop graph | torturous | 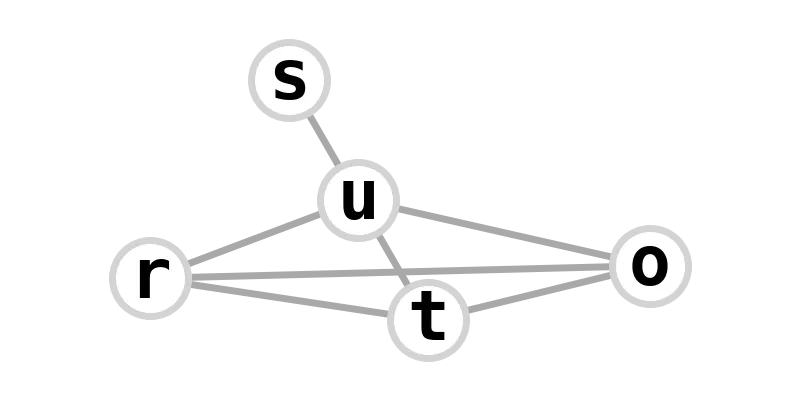 |
| cricket graph | aether | 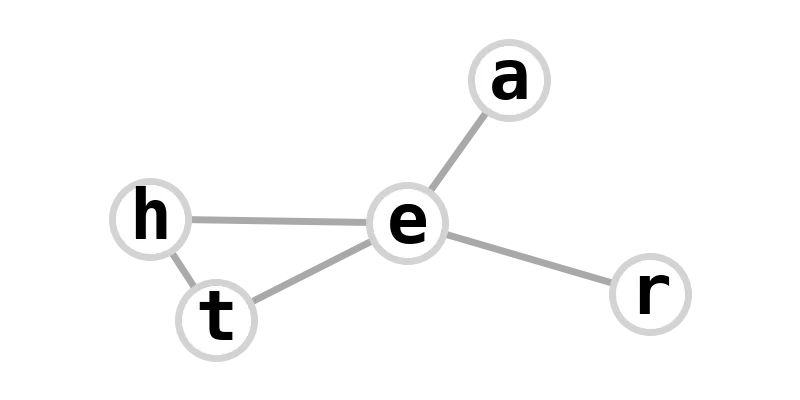 |
| 5-path | earth | 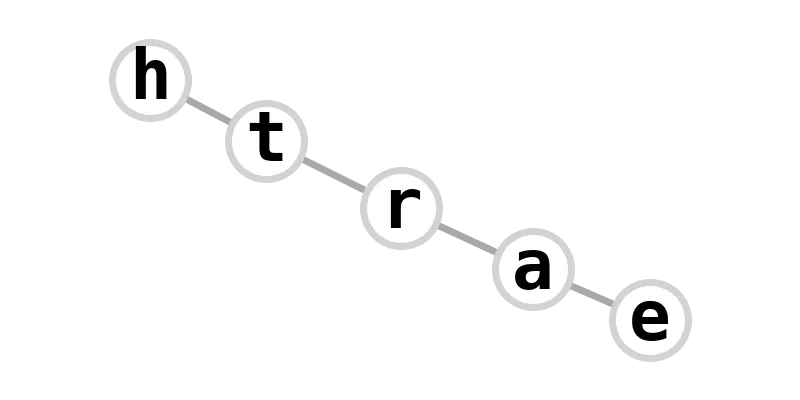 |
| dart graph | instant | 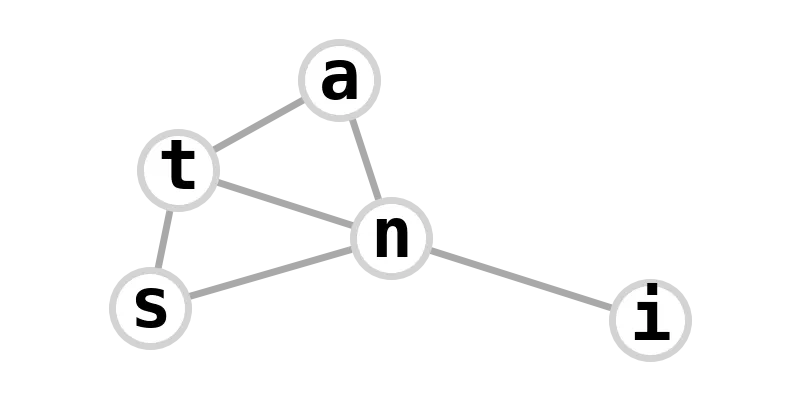 |
| 5-star | kabbalah | 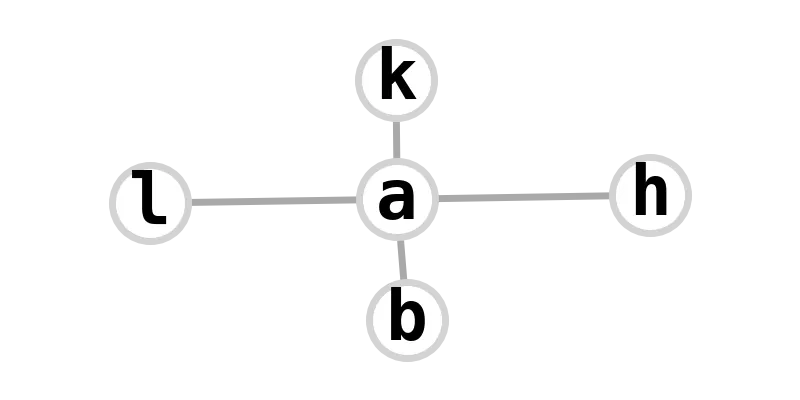 |
| gem graph | seascape | 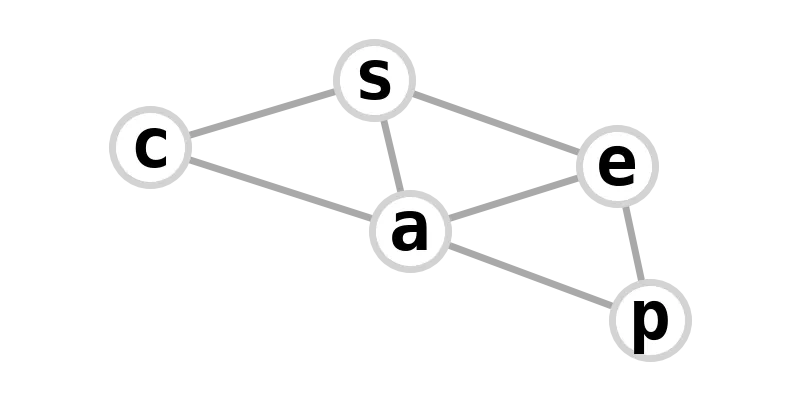 |
| (2,3)-complete bipartite | loyalty | 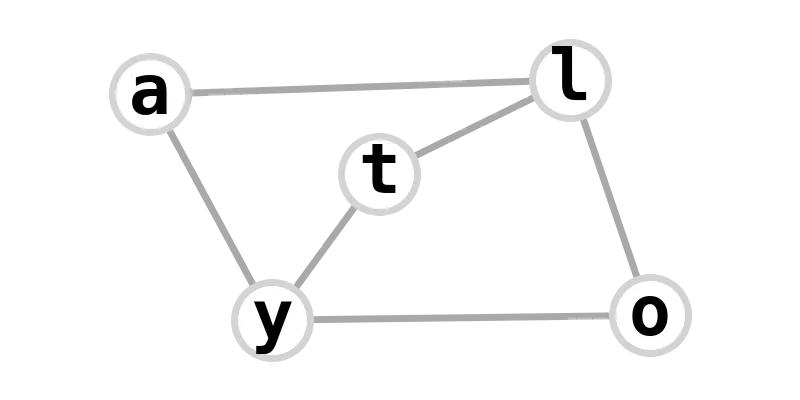 |
| house graph | automata | 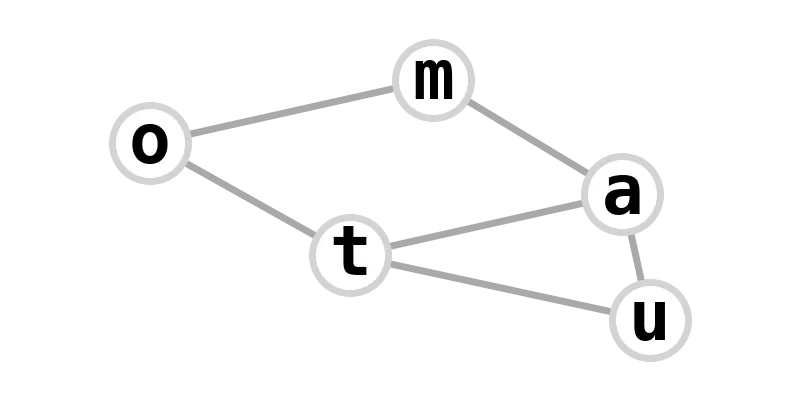 |
| (1,1,3)-complete tripartite | attractant | 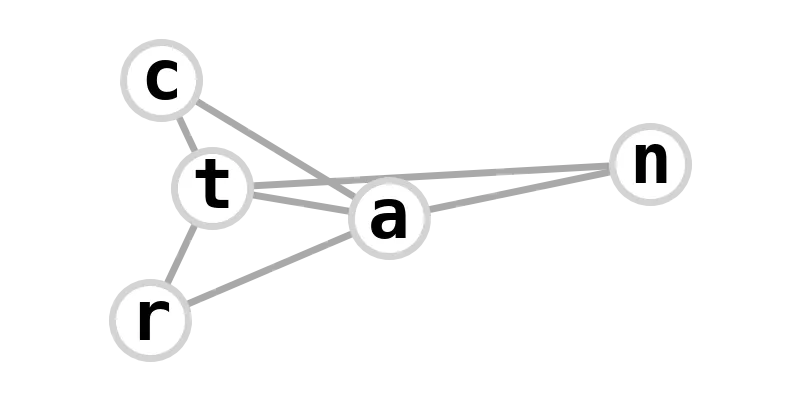 |
| house X graph | lanolin | 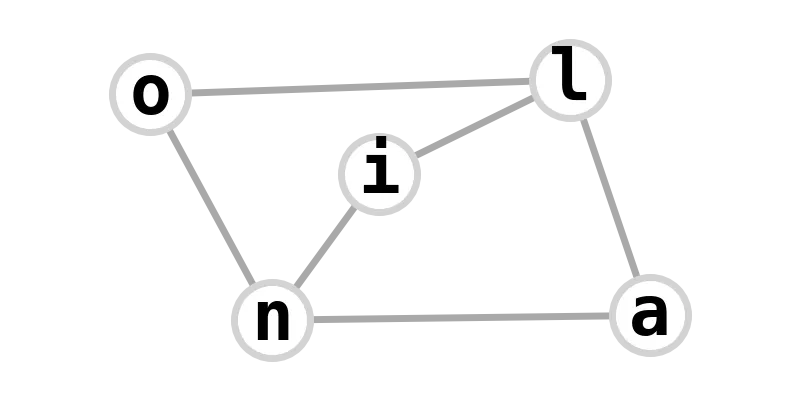 |
| 5-cycle (pentagon) | exhume | 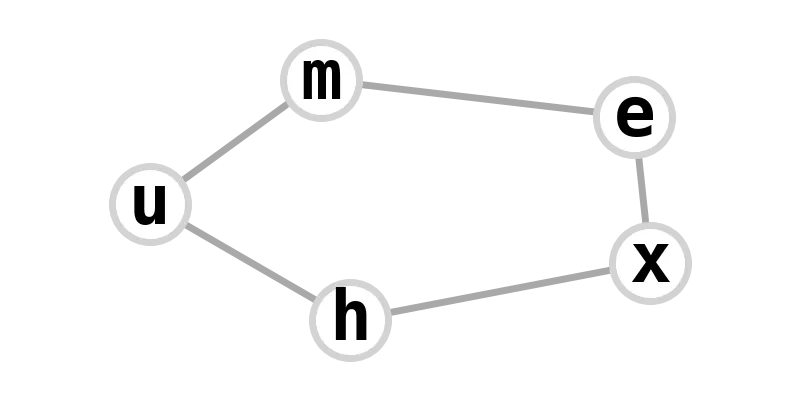 |
| 3-dipyramidal | intensities | 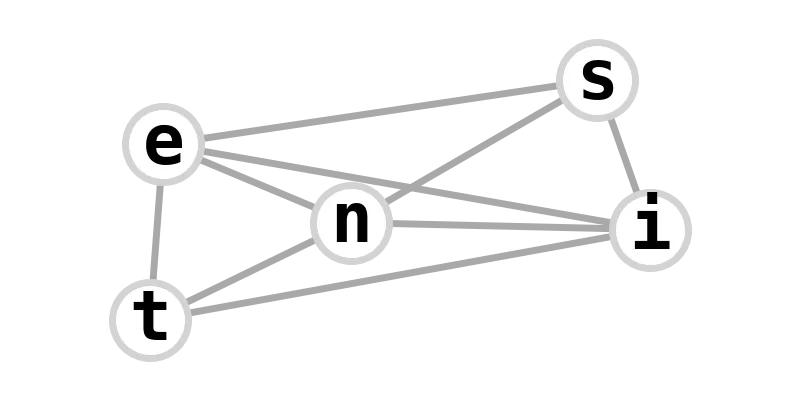 |
| 5-graph 31 | nurturant | 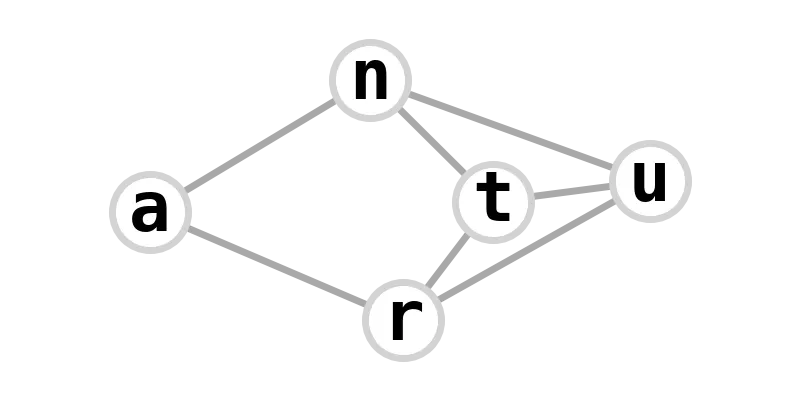 |
| 5-wheel | milliosmols | 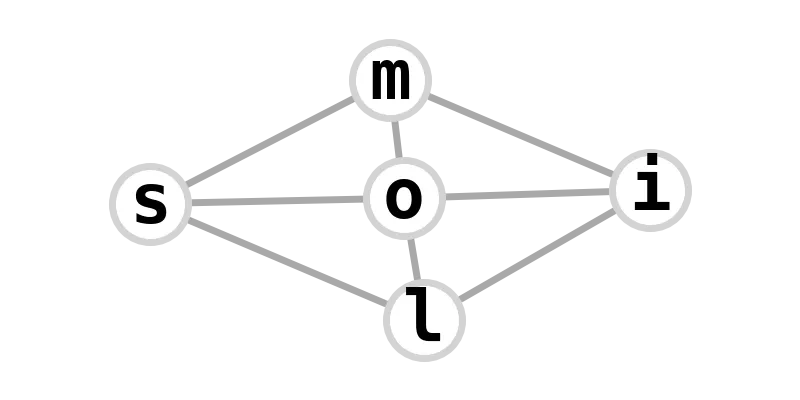 |
| K5 (pentatope) |  |
Names are taken from this page on Biconnected Graphs from Wolfram Mathworld.
6 Nodes
TODO
-
“Graph” as in “graph theory”, the study of networks and connections. To get a word’s letter-adjacency graph: Each letter is a vertex. There is an edge connecting two letters if they show up next to each other in the word. The graphs are simple graphs, meaning we don’t connect a letter to itself (in words like “moon”), nor do we add extra edges when the same adjacency happens multiple times (in words like “donor”). ↩